Divergent Series & Continued Fraction (from Gauss' Mathematical Diary)Summation methods for divergent seriesPoles from the Continued Fraction Expansion of the Tangent Function?A “couple” of questions on Gauss's mathematical diaryPalindromic continued fractionContinued fraction representation of ZetaDivision methods for divergent continued fractionsidentity which include continued fractionA family of divergent seriesThe Heine $q$-continued fractionContinued Fraction of Random Variables
Divergent Series & Continued Fraction (from Gauss' Mathematical Diary)
Summation methods for divergent seriesPoles from the Continued Fraction Expansion of the Tangent Function?A “couple” of questions on Gauss's mathematical diaryPalindromic continued fractionContinued fraction representation of ZetaDivision methods for divergent continued fractionsidentity which include continued fractionA family of divergent seriesThe Heine $q$-continued fractionContinued Fraction of Random Variables
$begingroup$
I've asked that question before on History of Science and Mathematics but haven't received an answer
Does someone have a reference or further explanation on Gauß' entry from May 24, 1796 in his mathematical diary (Mathematisches Tagebuch, full scan available via https://gdz.sub.uni-goettingen.de/id/DE-611-HS-3382323) on page 3 regarding the divergent series
$$1-2+8-64...$$
in relation to the continued fraction
$$frac11+frac21+frac21+frac81+frac121+frac321+frac561+128$$
He states also - if I read it correctly - Transformatio seriei which could mean series transformation, but I don't see how he transforms from the series to the continued fraction resp. which transformation or rule he applied.
The OEIS has an entry (https://oeis.org/A014236) for the sequence $2,2,8,12,32,56,128$, but I don't see the connection either.
My question: Can anyone help or clarify the relationship that Gauss' used?
Torsten Schoeneberg remarked rightfully in the original question that the term in the series are $(-1)^ncdot 2^frac12n(n+1)$ and Gerald Edgar conjectures it might be related to Gauss' Continued Fraction.
ho.history-overview gaussian continued-fractions divergent-series
$endgroup$
add a comment |
$begingroup$
I've asked that question before on History of Science and Mathematics but haven't received an answer
Does someone have a reference or further explanation on Gauß' entry from May 24, 1796 in his mathematical diary (Mathematisches Tagebuch, full scan available via https://gdz.sub.uni-goettingen.de/id/DE-611-HS-3382323) on page 3 regarding the divergent series
$$1-2+8-64...$$
in relation to the continued fraction
$$frac11+frac21+frac21+frac81+frac121+frac321+frac561+128$$
He states also - if I read it correctly - Transformatio seriei which could mean series transformation, but I don't see how he transforms from the series to the continued fraction resp. which transformation or rule he applied.
The OEIS has an entry (https://oeis.org/A014236) for the sequence $2,2,8,12,32,56,128$, but I don't see the connection either.
My question: Can anyone help or clarify the relationship that Gauss' used?
Torsten Schoeneberg remarked rightfully in the original question that the term in the series are $(-1)^ncdot 2^frac12n(n+1)$ and Gerald Edgar conjectures it might be related to Gauss' Continued Fraction.
ho.history-overview gaussian continued-fractions divergent-series
$endgroup$
add a comment |
$begingroup$
I've asked that question before on History of Science and Mathematics but haven't received an answer
Does someone have a reference or further explanation on Gauß' entry from May 24, 1796 in his mathematical diary (Mathematisches Tagebuch, full scan available via https://gdz.sub.uni-goettingen.de/id/DE-611-HS-3382323) on page 3 regarding the divergent series
$$1-2+8-64...$$
in relation to the continued fraction
$$frac11+frac21+frac21+frac81+frac121+frac321+frac561+128$$
He states also - if I read it correctly - Transformatio seriei which could mean series transformation, but I don't see how he transforms from the series to the continued fraction resp. which transformation or rule he applied.
The OEIS has an entry (https://oeis.org/A014236) for the sequence $2,2,8,12,32,56,128$, but I don't see the connection either.
My question: Can anyone help or clarify the relationship that Gauss' used?
Torsten Schoeneberg remarked rightfully in the original question that the term in the series are $(-1)^ncdot 2^frac12n(n+1)$ and Gerald Edgar conjectures it might be related to Gauss' Continued Fraction.
ho.history-overview gaussian continued-fractions divergent-series
$endgroup$
I've asked that question before on History of Science and Mathematics but haven't received an answer
Does someone have a reference or further explanation on Gauß' entry from May 24, 1796 in his mathematical diary (Mathematisches Tagebuch, full scan available via https://gdz.sub.uni-goettingen.de/id/DE-611-HS-3382323) on page 3 regarding the divergent series
$$1-2+8-64...$$
in relation to the continued fraction
$$frac11+frac21+frac21+frac81+frac121+frac321+frac561+128$$
He states also - if I read it correctly - Transformatio seriei which could mean series transformation, but I don't see how he transforms from the series to the continued fraction resp. which transformation or rule he applied.
The OEIS has an entry (https://oeis.org/A014236) for the sequence $2,2,8,12,32,56,128$, but I don't see the connection either.
My question: Can anyone help or clarify the relationship that Gauss' used?
Torsten Schoeneberg remarked rightfully in the original question that the term in the series are $(-1)^ncdot 2^frac12n(n+1)$ and Gerald Edgar conjectures it might be related to Gauss' Continued Fraction.
ho.history-overview gaussian continued-fractions divergent-series
ho.history-overview gaussian continued-fractions divergent-series
asked 9 hours ago
MarcusMarcus
561 silver badge5 bronze badges
561 silver badge5 bronze badges
add a comment |
add a comment |
1 Answer
1
active
oldest
votes
$begingroup$
The entry from May 24, 1796 is worked out in a more general form on February 16, 1797 [reproduced below from this scan]
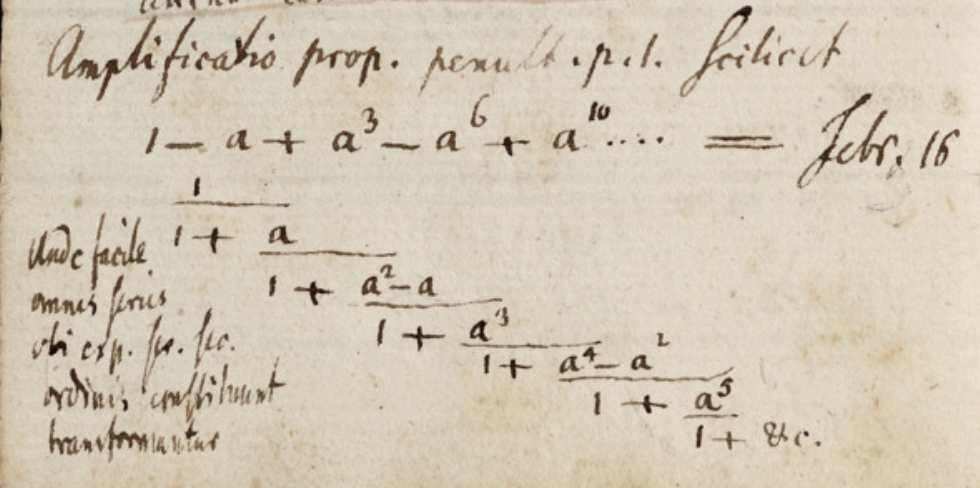
$$1-a+a^3-a^6+a^10+cdots=frac11+fraca1+fraca^2-a1+fraca^31+fraca^4-a^21+fraca^51+cdots$$
so the coefficients alternate between $a^2n+1$ and $a^2n-a^n$.
Latin text: Amplificatio prop[ositionis] penult[imae] p[aginae] 1, scilicet $cdots$
Unde facile omnes series ubi exp[onentes] ser[iem] sec[undi] ordinis constituunt transformantur.
Translation: Expanding on the proposition 1 from the next-to-last page $cdots$
From here one can easily transform every series the exponents of which form a series of the second order.
These continued fractions of series of the form
$$1+sum_n=1^infty a^n(n+1)-sum_n=1^infty a^n^2=sum_n=0^infty (-1)^n a^n(n+1)/2$$
are related to theta functions, see chapter 29 of "Series and Products from the Fifteenth to the Twenty-first Century". Apparently the series originated from Jakob Bernoulli (1690).
$endgroup$
$begingroup$
Great. Would you mind saying a bit more about the relation, and how to understand the continued fraction equality, for those who cannot see the google preview?
$endgroup$
– Torsten Schoeneberg
7 hours ago
add a comment |
Your Answer
StackExchange.ready(function()
var channelOptions =
tags: "".split(" "),
id: "504"
;
initTagRenderer("".split(" "), "".split(" "), channelOptions);
StackExchange.using("externalEditor", function()
// Have to fire editor after snippets, if snippets enabled
if (StackExchange.settings.snippets.snippetsEnabled)
StackExchange.using("snippets", function()
createEditor();
);
else
createEditor();
);
function createEditor()
StackExchange.prepareEditor(
heartbeatType: 'answer',
autoActivateHeartbeat: false,
convertImagesToLinks: true,
noModals: true,
showLowRepImageUploadWarning: true,
reputationToPostImages: 10,
bindNavPrevention: true,
postfix: "",
imageUploader:
brandingHtml: "Powered by u003ca class="icon-imgur-white" href="https://imgur.com/"u003eu003c/au003e",
contentPolicyHtml: "User contributions licensed under u003ca href="https://creativecommons.org/licenses/by-sa/3.0/"u003ecc by-sa 3.0 with attribution requiredu003c/au003e u003ca href="https://stackoverflow.com/legal/content-policy"u003e(content policy)u003c/au003e",
allowUrls: true
,
noCode: true, onDemand: true,
discardSelector: ".discard-answer"
,immediatelyShowMarkdownHelp:true
);
);
Sign up or log in
StackExchange.ready(function ()
StackExchange.helpers.onClickDraftSave('#login-link');
);
Sign up using Google
Sign up using Facebook
Sign up using Email and Password
Post as a guest
Required, but never shown
StackExchange.ready(
function ()
StackExchange.openid.initPostLogin('.new-post-login', 'https%3a%2f%2fmathoverflow.net%2fquestions%2f334869%2fdivergent-series-continued-fraction-from-gauss-mathematical-diary%23new-answer', 'question_page');
);
Post as a guest
Required, but never shown
1 Answer
1
active
oldest
votes
1 Answer
1
active
oldest
votes
active
oldest
votes
active
oldest
votes
$begingroup$
The entry from May 24, 1796 is worked out in a more general form on February 16, 1797 [reproduced below from this scan]
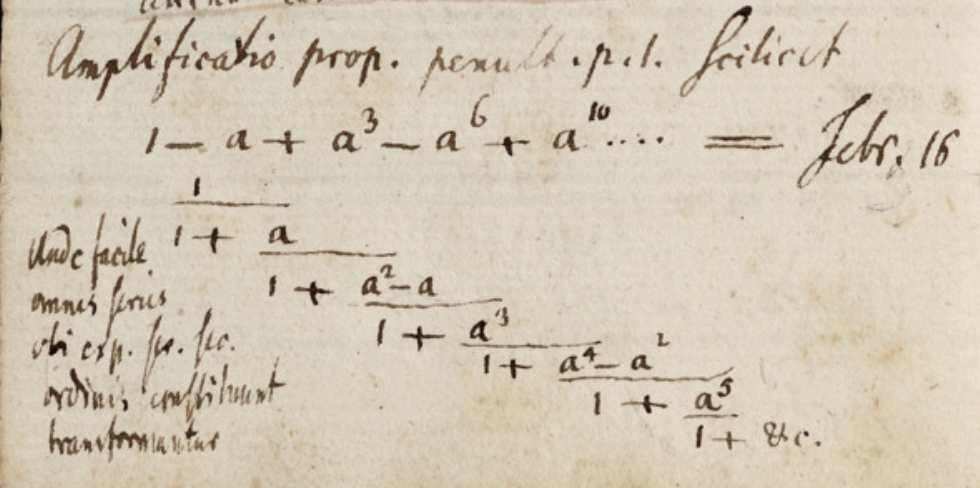
$$1-a+a^3-a^6+a^10+cdots=frac11+fraca1+fraca^2-a1+fraca^31+fraca^4-a^21+fraca^51+cdots$$
so the coefficients alternate between $a^2n+1$ and $a^2n-a^n$.
Latin text: Amplificatio prop[ositionis] penult[imae] p[aginae] 1, scilicet $cdots$
Unde facile omnes series ubi exp[onentes] ser[iem] sec[undi] ordinis constituunt transformantur.
Translation: Expanding on the proposition 1 from the next-to-last page $cdots$
From here one can easily transform every series the exponents of which form a series of the second order.
These continued fractions of series of the form
$$1+sum_n=1^infty a^n(n+1)-sum_n=1^infty a^n^2=sum_n=0^infty (-1)^n a^n(n+1)/2$$
are related to theta functions, see chapter 29 of "Series and Products from the Fifteenth to the Twenty-first Century". Apparently the series originated from Jakob Bernoulli (1690).
$endgroup$
$begingroup$
Great. Would you mind saying a bit more about the relation, and how to understand the continued fraction equality, for those who cannot see the google preview?
$endgroup$
– Torsten Schoeneberg
7 hours ago
add a comment |
$begingroup$
The entry from May 24, 1796 is worked out in a more general form on February 16, 1797 [reproduced below from this scan]
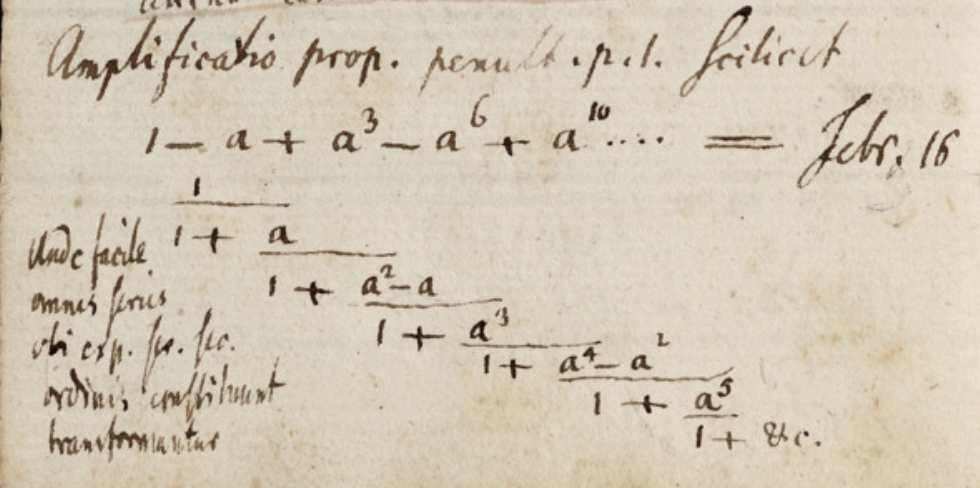
$$1-a+a^3-a^6+a^10+cdots=frac11+fraca1+fraca^2-a1+fraca^31+fraca^4-a^21+fraca^51+cdots$$
so the coefficients alternate between $a^2n+1$ and $a^2n-a^n$.
Latin text: Amplificatio prop[ositionis] penult[imae] p[aginae] 1, scilicet $cdots$
Unde facile omnes series ubi exp[onentes] ser[iem] sec[undi] ordinis constituunt transformantur.
Translation: Expanding on the proposition 1 from the next-to-last page $cdots$
From here one can easily transform every series the exponents of which form a series of the second order.
These continued fractions of series of the form
$$1+sum_n=1^infty a^n(n+1)-sum_n=1^infty a^n^2=sum_n=0^infty (-1)^n a^n(n+1)/2$$
are related to theta functions, see chapter 29 of "Series and Products from the Fifteenth to the Twenty-first Century". Apparently the series originated from Jakob Bernoulli (1690).
$endgroup$
$begingroup$
Great. Would you mind saying a bit more about the relation, and how to understand the continued fraction equality, for those who cannot see the google preview?
$endgroup$
– Torsten Schoeneberg
7 hours ago
add a comment |
$begingroup$
The entry from May 24, 1796 is worked out in a more general form on February 16, 1797 [reproduced below from this scan]
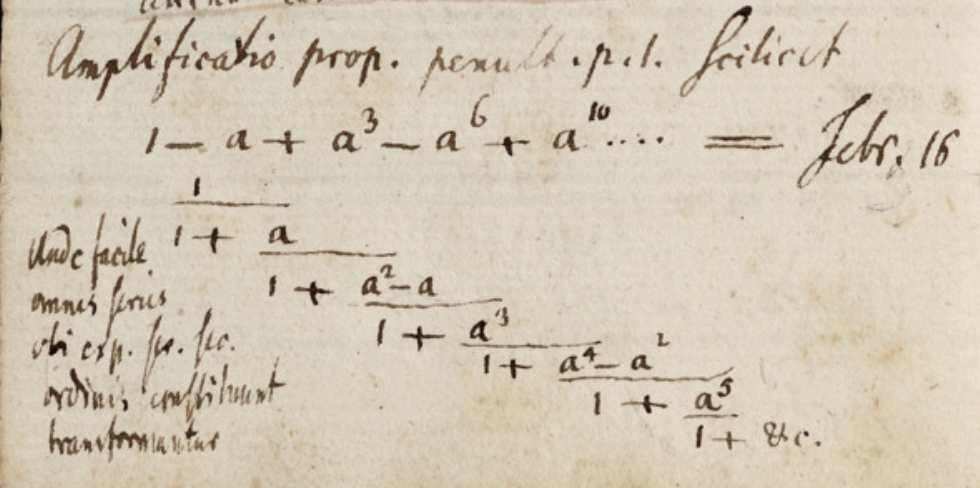
$$1-a+a^3-a^6+a^10+cdots=frac11+fraca1+fraca^2-a1+fraca^31+fraca^4-a^21+fraca^51+cdots$$
so the coefficients alternate between $a^2n+1$ and $a^2n-a^n$.
Latin text: Amplificatio prop[ositionis] penult[imae] p[aginae] 1, scilicet $cdots$
Unde facile omnes series ubi exp[onentes] ser[iem] sec[undi] ordinis constituunt transformantur.
Translation: Expanding on the proposition 1 from the next-to-last page $cdots$
From here one can easily transform every series the exponents of which form a series of the second order.
These continued fractions of series of the form
$$1+sum_n=1^infty a^n(n+1)-sum_n=1^infty a^n^2=sum_n=0^infty (-1)^n a^n(n+1)/2$$
are related to theta functions, see chapter 29 of "Series and Products from the Fifteenth to the Twenty-first Century". Apparently the series originated from Jakob Bernoulli (1690).
$endgroup$
The entry from May 24, 1796 is worked out in a more general form on February 16, 1797 [reproduced below from this scan]
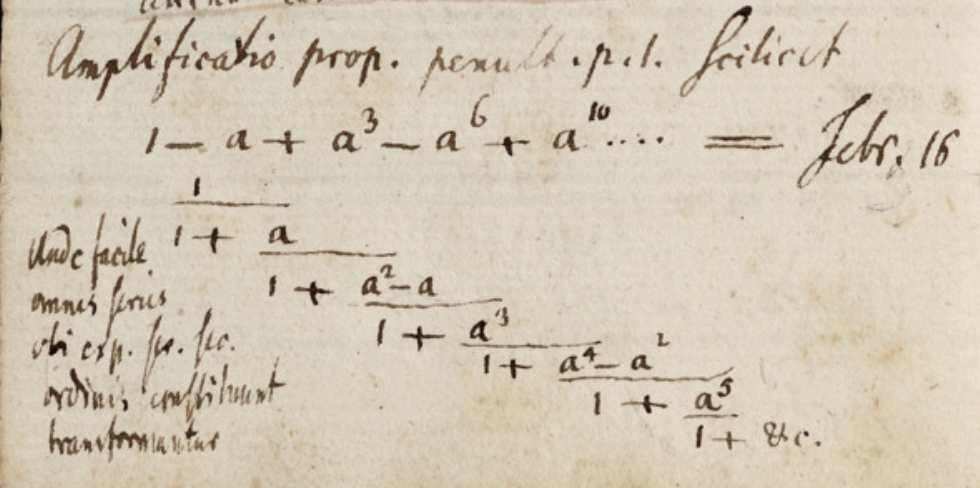
$$1-a+a^3-a^6+a^10+cdots=frac11+fraca1+fraca^2-a1+fraca^31+fraca^4-a^21+fraca^51+cdots$$
so the coefficients alternate between $a^2n+1$ and $a^2n-a^n$.
Latin text: Amplificatio prop[ositionis] penult[imae] p[aginae] 1, scilicet $cdots$
Unde facile omnes series ubi exp[onentes] ser[iem] sec[undi] ordinis constituunt transformantur.
Translation: Expanding on the proposition 1 from the next-to-last page $cdots$
From here one can easily transform every series the exponents of which form a series of the second order.
These continued fractions of series of the form
$$1+sum_n=1^infty a^n(n+1)-sum_n=1^infty a^n^2=sum_n=0^infty (-1)^n a^n(n+1)/2$$
are related to theta functions, see chapter 29 of "Series and Products from the Fifteenth to the Twenty-first Century". Apparently the series originated from Jakob Bernoulli (1690).
edited 7 hours ago
answered 8 hours ago
Carlo BeenakkerCarlo Beenakker
84.4k9 gold badges199 silver badges305 bronze badges
84.4k9 gold badges199 silver badges305 bronze badges
$begingroup$
Great. Would you mind saying a bit more about the relation, and how to understand the continued fraction equality, for those who cannot see the google preview?
$endgroup$
– Torsten Schoeneberg
7 hours ago
add a comment |
$begingroup$
Great. Would you mind saying a bit more about the relation, and how to understand the continued fraction equality, for those who cannot see the google preview?
$endgroup$
– Torsten Schoeneberg
7 hours ago
$begingroup$
Great. Would you mind saying a bit more about the relation, and how to understand the continued fraction equality, for those who cannot see the google preview?
$endgroup$
– Torsten Schoeneberg
7 hours ago
$begingroup$
Great. Would you mind saying a bit more about the relation, and how to understand the continued fraction equality, for those who cannot see the google preview?
$endgroup$
– Torsten Schoeneberg
7 hours ago
add a comment |
Thanks for contributing an answer to MathOverflow!
- Please be sure to answer the question. Provide details and share your research!
But avoid …
- Asking for help, clarification, or responding to other answers.
- Making statements based on opinion; back them up with references or personal experience.
Use MathJax to format equations. MathJax reference.
To learn more, see our tips on writing great answers.
Sign up or log in
StackExchange.ready(function ()
StackExchange.helpers.onClickDraftSave('#login-link');
);
Sign up using Google
Sign up using Facebook
Sign up using Email and Password
Post as a guest
Required, but never shown
StackExchange.ready(
function ()
StackExchange.openid.initPostLogin('.new-post-login', 'https%3a%2f%2fmathoverflow.net%2fquestions%2f334869%2fdivergent-series-continued-fraction-from-gauss-mathematical-diary%23new-answer', 'question_page');
);
Post as a guest
Required, but never shown
Sign up or log in
StackExchange.ready(function ()
StackExchange.helpers.onClickDraftSave('#login-link');
);
Sign up using Google
Sign up using Facebook
Sign up using Email and Password
Post as a guest
Required, but never shown
Sign up or log in
StackExchange.ready(function ()
StackExchange.helpers.onClickDraftSave('#login-link');
);
Sign up using Google
Sign up using Facebook
Sign up using Email and Password
Post as a guest
Required, but never shown
Sign up or log in
StackExchange.ready(function ()
StackExchange.helpers.onClickDraftSave('#login-link');
);
Sign up using Google
Sign up using Facebook
Sign up using Email and Password
Sign up using Google
Sign up using Facebook
Sign up using Email and Password
Post as a guest
Required, but never shown
Required, but never shown
Required, but never shown
Required, but never shown
Required, but never shown
Required, but never shown
Required, but never shown
Required, but never shown
Required, but never shown