Ώσμωση ονομάζεται το φαινόμενο της διέλευσης περισσότερων μορίων διαλύτη, μέσω ημιπερατής μεμβράνης, από τον διαλύτη στο διάλυμα ή από το διάλυμα μικρότερης συγκέντρωσης (αραιότερο) προς το διάλυμα μεγαλύτερης συγκέντρωσης σε διαλυμένη ουσία (πυκνότερο). Ημιπερατή είναι η μεμβράνη που επιτρέπει να περνούν μέσα από τους πόρους της τα μόρια του διαλύτη, αλλά δεν επιτρέπει να περνούν τα μόρια της διαλυμένης ουσίας. Ημιπερατές μεμβράνες υπάρχουν και φυσικές (π.χ. η κυτταρική μεμβράνη) και συνθετικές (π.χ. το σελοφάν).

Η ώσμωση είναι μια φυσική διαδικασία κατά την οποία ο διαλύτης κινείται, αυθόρμητα, μέσω μεμβράνης που είναι διαπερατή για τα μόριά του όχι όμως και για τα μόρια της διαλυμένης ουσίας και διαχωρίζει δύο διαλύματα διαφορετικών συγκεντρώσεων ή χωρίζει ένα διαλύτη από ένα διάλυμα. Χωρίς την ύπαρξη της μεμβράνης θα συνέβαινε απλή ανάμιξη των δύο διαλυμάτων ή του διαλύτη και του διαλύματος. Αν από την ημιπερατή μεμβράνη περνά και διαλυμένη ουσία, τότε η διαδικασία παύει να είναι ώσμωση και γίνεται διάχυση μεταξύ των δύο διαλυμάτων.

Η ώσμωση πραγματοποιείται με σκοπό να εξισωθούν οι συγκεντρώσεις των διαλυμάτων από τις δύο πλευρές της ημιπερατής μεμβράνης. Το φαινόμενο της ώσμωσης είναι πολύ σημαντικό στα διάφορα βιολογικά συστήματα, καθώς πολλές βιολογικές μεμβράνες είναι ημιπερατές.

Ιστορικά στοιχεία |

Jacobus Henricus van't Hoff (1852-1911)

Σ' ένα έγγραφο του 1682 ο Ρόμπερτ Μπόυλ (Robert Boyle) αναφέρει για πρώτη φορά φαινόμενα ώσμωσης αλλά οι πρώτες παρατηρήσεις έγιναν το 1748 από τον Αβά Νολλέ (Abbe Nollet), ο οποίος πήρε ένα κύλινδρο με κρασί και σκέπασε το στόμιό του με κύστη ζώου. Στη συνέχεια βύθισε τον κύλινδρο μέσα σε νερό και παρατήρησε ότι περνούσε νερό μέσα από την κύστη και έμπαινε στο κρασί. Αυτό του έκανε εντύπωση και αναρωτήθηκε ποια ήταν η δύναμη που προκαλούσε τη μετακίνηση του νερού. Έπρεπε να δοθεί μάλιστα και κάποιο σοβαρό όνομα με ελληνική ρίζα και έτσι ονομάστηκε ωσμωτική (από το ρήμα ωθώ) πίεση.

Οι πρώτες συστηματικές μελέτες του φαινομένου της ώσμωσης (για την ακρίβεια οι πρώτες μετρήσεις της ωσμωτικής πίεσης αποδίδονται στους βοτανολόγους Πφέφφερ (Wilhelm Pfeffer) και ντε Βρις (Hugo de Vries) οι οποίοι μέτρησαν την ωσμωτική πίεση με την εύρεση της υδροστατικής πίεσης που προκαλείται από τη στήλη h (βλέπε παρακάτω) το 1877. Σε άλλα πιο σημαντικά πειράματα ο Pfeffer χρησιμοποίησε ειδική διάταξη γνωστή ως ωσμόμετρο του Pfeffer με ειδική ημιπερατή μεμβράνη που επινοήθηκε από τον Τράουμπε (M. Traube).

Τα πειράματα του Pfeffer, ιδίως στα υδατικά διαλύματα ζάχαρης, έδωσαν αφορμή στον Ολλανδό χημικό βαν'τ Χοφ (Jacobus Henricus van't Hoff) να ασχοληθεί με την ωσμωτική πίεση που είναι ιδιαίτερα θεαματική στα φυτά, αφού οι χυμοί τους ανυψώνονται σε ύψος δεκάδων μέτρων. Ήδη ήταν γνωστός ο νόμος των τέλειων αερίων (PV=RT) αλλά ο van't Hoff εισάγοντας στο δεύτερο μέλος της εξίσωσης έναν συντελεστή i, μπόρεσε να εξηγήσει καλύτερα τα φαινόμενα. Την ορθή ερμηνεία του παράγοντα i, δηλαδή ότι αποτελεί μέτρο της ιοντικής διάστασης, υπέδειξε ο Σβάντε Αρρένιους με γράμμα του προς τον van't Hoff. Ο τελευταίος ασπάσθηκε με ενθουσιασμό την άποψη αυτή και δε δίστασε στην επόμενη εργασία του να εξάρει το ρόλο του Αρρένιους. Οι θεωρίες του van't Hoff για την ώσμωση μαζί με τις εργασίες του στη Θερμοδυναμική και Χημική Κινητική που προηγήθηκαν, έφεραν σ' αυτόν το πρώτο βραβείο Νόμπελ Χημείας το 1901.

Περιγραφή του φαινομένου |

Για την καλύτερη μελέτη και εξήγηση της ώσμωσης, διακρίνουμε δύο περιπτώσεις διαλυμάτων που χωρίζονται με ημιπερατή μεμβράνη :

Φέρονται σε επαφή (βλέπε σχήμα), μέσω ημιπερατής μεμβράνης, ένα υδατικό διάλυμα κάποιας χημικής ένωσης (π.χ. ζάχαρης) συγκέντρωσης C^[1] και καθαρός διαλύτης (που θεωρούμε ότι έχει συγκέντρωση σε διαλυμένη ουσία C=0)^[2] (νερό). Αρχικά η ταχύτητα μετακίνησης (υ₁) των μορίων του νερού από τον καθαρό διαλύτη προς το διάλυμα είναι μεγαλύτερη από την ταχύτητα μετακίνησης (υ₂) των μορίων του νερού από το διάλυμα προς τον καθαρό διαλύτη. Δηλαδή αρχικά είναι υ₁ > υ₂. Έτσι, ο όγκος του διαλύματος αυξάνεται, οπότε παρατηρείται ανύψωση της στάθμης του διαλύματος μέσα στο δεξιό τμήμα του δοχείου. Το φαινόμενο της ώσμωσης θα συνεχιστεί με σκοπό να εξισωθούν οι συγκεντρώσεις από τις δύο πλευρές της ημιπερατής μεμβράνης. Αυτό όμως δε μπορεί να συμβεί, διότι ο καθαρός διαλύτης δεν περιέχει διαλυμένη ουσία.

Με το πέρασμα του χρόνου, η ανύψωση της στάθμης του διαλύματος επιβραδύνεται και τελικά σταθεροποιείται σε ορισμένο ύψος (h) οπότε και σταματά το φαινόμενο της ώσμωσης. Αυτό συμβαίνει διότι η υδροστατική πίεση (Ρ_υδρ = ε.h) που δημιουργείται, λόγω της ανύψωσης της στάθμης και οφείλεται στη στήλη του διαλύματος ύψους h, εξαναγκάζει τα μόρια του διαλύτη να εξέρχονται με την ίδια ταχύτητα με την οποία εισέρχονται. Δηλαδή τελικά αποκαθίσταται κατάσταση δυναμικής ισορροπίας όπου υ₁ = υ₂.

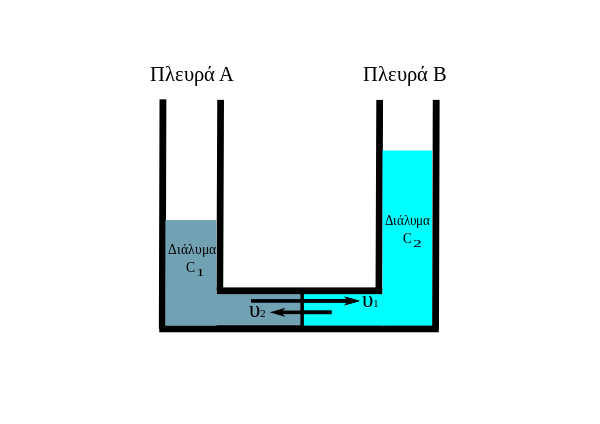
Τα δύο τμήματα του δοχείου περιέχουν διαλύματα της ίδια ουσίας αλλά διαφορετικών συγκεντρώσεων C₁ (αραιότερο) και C₂ (πυκνότερο) και ισχύει C₁ < C₂. Αρχικά η ταχύτητα διάχυσης των μορίων του διαλύτη από το αραιότερο προς το πυκνότερο διάλυμα είναι μεγάλη. Έτσι θα συμβεί ώσμωση από το διάλυμα με συγκέντρωση C₁ προς το διάλυμα συγκέντρωσης C₂. Το φαινόμενο της ώσμωσης θα συνεχιστεί μέχρι να εξισωθούν οι συγκεντρώσεις των διαλυμάτων από τις δύο πλευρές της μεμβράνης, δηλαδή μέχρι να γίνει C₁' = C₂' όπου C₁' και C₂' οι νέες συγκεντρώσεις όταν σταματήσει η ώσμωση. Στο σημείο αυτό αποκαθίσταται δυναμική ισορροπία, δηλαδή ίδιος αριθμός μορίων διαλύτη περνά μέσα από την ημιπερατή μεμβράνη στη μονάδα του χρόνου και προς τις δύο κατευθύνσεις (δηλαδή υ₁ = υ₂). Το φαινόμενο μπορεί να σταματήσει επίσης αν τα δύο διαλύματα έχουν μεγάλη διαφορά συγκεντρώσεων και η υδροστατική στήλη (βλέπε προηγούμενη παράγραφο) είναι τόσο ψηλή που σταματά την ώσμωση εμποδίζοντας τη διέλευση των μορίων του διαλύτη πριν εξισωθούν οι συγκεντρώσεις.

Φυσικά δεν παρατηρείται ώσμωση αν από την αρχή τα δύο διαλύματα έχουν ίδιες συγκεντρώσεις δηλ. είναι αρχικά C₁ = C₂.

Θερμοδυναμική ερμηνεία της ώσμωσης |

Παλαιότερα επικρατούσε η άποψη ότι το νερό και όχι η διαλυμένη ουσία περνούσε από τη μια πλευρά της μεμβράνης στην άλλη επειδή οι πόροι της ημιπερατής μεμβράνης ήταν μεγαλύτεροι από τα μόρια του νερού αλλά μικρότεροι από τα μόρια της διαλυμένης ουσίας. Σήμερα γίνεται δεκτό ότι η διέλευση μορίων νερού οφείλεται καθαρά σε ηλεκτροστατικούς λόγους. Επίσης πρέπει να τονιστεί ότι η διαλυμένη ουσία δεν παίζει κανένα ρόλο στα φαινόμενα ώσμωσης.

Για την καλύτερη εξήγηση διέλευσης του νερού από την πλευρά που αυτό είναι καθαρό ή βρίσκεται σε διάλυμα μικρότερης συγκέντρωσης προς την πλευρά του διαλύματος μεγαλύτερης συγκέντρωσης, θα θεωρήσουμε ότι η ποσότητα του καθαρού νερού αλλά και του νερού ως διαλύτη στο διάλυμα είναι 1 mol^[3] και θα ονομάσουμε :

"πλευρά Α" τη μεριά του καθαρού νερού ή του αραιότερου διαλύματος (αριστερή μεριά #Περιγραφή του φαινομένου) και

"πλευρά Β" τη μεριά του πυκνότερου διαλύματος (δεξιά μεριά #Περιγραφή του φαινομένου)

Οι δύο πλευρές χωρίζονται με ημιπερατή μεμβράνη.

Εξήγηση με βάση το ρυθμό κρούσης των μορίων του νερού στη μεμβράνη |

Όταν και από τις δύο πλευρές της μεμβράνης υπάρχει καθαρό νερό, τα μόριά του διέρχονται με τον ίδιο ρυθμό και προς τις δύο κατευθύνσεις, οπότε μακροσκοπικά δεν παρατηρείται ροή νερού και ο όγκος του νερού στα δύο τμήματα του δοχείου δε μεταβάλλεται.

Όταν όμως από τη πλευρά Β της ημιπερατής μεμβράνης υπάρχει κάποιο διάλυμα, τότε τα μόρια της διαλυμένης ουσίας αφενός δε μπορούν να διέλθουν από τη μεμβράνη (για ηλεκτροστατικούς λόγους), αφετέρου παρεμποδίζουν τα μόρια του νερού και αυτά δε χτυπούν στη μεμβράνη με τον ίδιο ρυθμό όπως τα μόρια από την πλευρά Α. Έτσι τα μόρια του νερού διέρχονται από την πλευρά Α προς την πλευρά Β με μεγαλύτερο ρυθμό από ότι ανάποδα με συνέπεια να αυξάνεται ο όγκος προς την πλευρά Β. Αυτή η καθαρή ροή νερού θα επιβραδυνθεί και τελικά θα σταματήσει όταν η πίεση από τη στήλη διαλύματος που δημιουργείται στην πλευρά Β θα γίνει τόση ώστε οι ρυθμοί διέλευσης νερού και προς τις δύο κατευθύνσεις να εξισωθούν. Τότε θα υπάρξει δυναμική (και όχι στατική) ισορροπία αφού στη μονάδα του χρόνου όσα μόρια νερού περνούν από την πλευρά Α στη Β, ακριβώς τόσα θα περνούν και από τη Β στην Α.

Εξήγηση με βάση την έννοια του χημικού δυναμικού |

Χημικό δυναμικό ενός συστατικού i σε ένα διάλυμα ονομάζεται η μερική γραμμομοριακή ελεύθερη ενέργεια του συστατικού αυτού στο διάλυμα. Το χημικό δυναμικό αποτελεί μέτρο χημικής σταθερότητας και μπορεί να χρησιμοποιηθεί για την πρόβλεψη και ερμηνεία των αλλαγών φάσεων και των χημικών αντιδράσεων. Ουσίες με υψηλότερο δυναμικό θα αντιδράσουν ή θα μετατραπούν από τη μια φάση στην άλλη με σκοπό να μειώσουν τη συνολική ελεύθερη ενέργεια Gibbs του συστήματος.

Έστω μ_Α το χημικό δυναμικό του καθαρού διαλύτη (πλευρά Α). Τότε το χημικό δυναμικό μ_Β του διαλύτη στο διάλυμα (πλευρά Β) θα είναι :

όπου :

• R = η παγκόσμια σταθερά των αερίων.


• T = η απόλυτη θερμοκρασία.


• N_B = το γραμμομοριακό κλάσμα ^[4] του διαλύτη στο διάλυμα (πλευρά Β). Ο όρος ln υποδηλώνει το νεπέρειο λογάριθμο.

Εφόσον σε ένα διάλυμα ισχύει πάντα N_B < 1 θα είναι και lnN_B < 0, οπότε αφού πάντα ισχύει RT > 0 συμπεραίνουμε ότι RTlnN_B < 0 και επομένως :

Άρα για να υπάρξει εξίσωση των χημικών δυναμικών και κατά συνέπεια θερμοδυναμική σταθερότητα, πρέπει να υπάρξει ροή μορίων νερού από την πλευρά Α (περιοχή υψηλού δυναμικού) προς την πλευρά Β (περιοχή χαμηλού δυναμικού).

Εξήγηση με βάση την έννοια της ελεύθερης ενέργειας |

Η ελεύθερη ενέργεια μιας ουσίας αντιπροσωπεύει την ενέργεια της ουσίας που μπορεί να μετατραπεί σε έργο, δηλαδή, το μέγιστο διαθέσιμο χρήσιμο έργο της ουσίας. Μια από τις εκφράσεις της είναι η ίδια με αυτή του χημικού δυναμικού.

Έστω G_A η ελεύθερη ενέργεια του καθαρού διαλύτη (πλευρά Α). Τότε η ελεύθερη ενέργεια G_B του διαλύτη στο διάλυμα (πλευρά Β) θα είναι, εντελώς ανάλογα με την περίπτωση του χημικού δυναμικού :

όπου τα σύμβολα είναι τα ίδια με του χημικού δυναμικού.

Άρα :

Πράγματι λοιπόν η διέλευση νερού από την πλευρά Α στη Β συνοδεύεται από ελάττωση της ελεύθερης ενέργειας, οπότε αποτελεί αυθόρμητη διεργασία.

Εξήγηση με βάση την έννοια της εντροπίας |

Το φαινόμενο της ώσμωσης μπορεί να εξηγηθεί και με τη χρήση της έννοιας της εντροπίας, από τη στατιστική μηχανική :

Η μεταβολή της εντροπίας ΔS_mix κατά την ανάμιξη καθαρού διαλύτη (από την πλευρά Α) και διαλύματος (της πλευράς Β) βάσει της θερμοδυναμικής εξίσωσης του Gibbs θα είναι :

Αφού n_BlnN_B < 0 και nlnN < 0 και R > 0 συμπεραίνουμε n_BlnN_B + nlnN < 0 και επομένως :

Πράγματι λοιπόν η ανάμιξη των συστατικών με μετακίνηση μορίων νερού από την πλευρά Α προς την πλευρά Β συνοδεύεται από αύξηση της εντροπίας και επομένως αποτελεί αυθόρμητη διεργασία.

Ωσμωτική πίεση |

Για να μη συμβεί ώσμωση μπορούμε να ασκήσουμε εξωτερική πίεση (Ρ_εξ) ίση με την ωσμωτική δηλ. Ρ_εξ = Π

'Ωσμωτική πίεση (Π) διαλύματος, που διαχωρίζεται με ημιπερατή μεμβράνη από τον καθαρό διαλύτη, ονομάζεται η ελάχιστη πίεση που πρέπει να ασκηθεί εξωτερικά στο διάλυμα, ώστε να εμποδιστεί το φαινόμενο της ώσμωσης, χωρίς να μεταβληθεί ο όγκος του διαλύματος.

Γενικά η ωσμωτική πίεση είναι μεγάλη, π.χ. για υδατικό διάλυμα καλαμοσάκχαρου 1 % w/v στους 15 °C είναι 0,684 atm. Στα φυτικά κύτταρα μπορεί να είναι μεταξύ 5 και 10 atm. Η ωσμωτική πίεση του αίματος στους 0° είναι 6,74 atm και οφείλεται κατά κύριο λόγο στα διάφορα ανόργανα άλατα που βρίσκονται στο πλάσμα σημαντικότερο των οποίων είναι το χλωριούχο νάτριο.

Η ώσμωση μπορεί να σταματήσει :

• Όταν η στήλη του διαλύματος στο σωλήνα στην πλευρά Β ανεβεί αρκετά, ώστε η υδροστατική πίεση της στήλης να αναγκάσει τα μόρια του διαλύτη να εξέρχονται προς την πλευρά Α με την ίδια ταχύτητα με την οποία εισέρχονται στην πλευρά Β.


• Αν από την αρχή είχε ασκηθεί στο διάλυμα στην πλευρά Β η κατάλληλη εξωτερική πίεση. Η ωσμωτική πίεση αναφέρεται σ' αυτή την περίπτωση. Η εξωτερική πίεση που απαιτείται είναι ίση με την υδροστατική πίεση (Ρ_υδρ = ε.h) που δημιουργείται από την ανύψωση της στάθμης του διαλύματος όταν το φαινόμενο έχει καταλήξει σε ισορροπία (βλέπε #Περιγραφή του φαινομένου).

Μεταξύ δύο διαλυμάτων :

• 
  Ισοτονικά ονομάζονται αν έχουν την ίδια τιμή ωσμωτικής πίεσης.

• 
  Υποτονικό ονομάζεται το διάλυμα που έχει τη μικρότερη τιμή ωσμωτικής πίεσης.

• 
  Υπερτονικό ονομάζεται το διάλυμα που έχει τη μεγαλύτερη τιμή ωσμωτικής πίεσης.

Νόμος του van't Hoff για την ωσμωτική πίεση σε μη ηλεκτρολυτικά (μοριακά) διαλύματα |

1) Αραιά μοριακά διαλύματα

Από τα πειραματικά αποτελέσματα του Pfeffer, ο van't Hoff διαπίστωσε ότι :

• το γινόμενο της ωσμωτικής πίεσης επί τον όγκο ενός διαλύματος για ορισμένη μάζα ζάχαρης και σε ορισμένη θερμοκρασία ήταν σταθερό δηλ. ΠV = σταθ.


• η ωσμωτική πίεση ορισμένου διαλύματος ζάχαρης ήταν ανάλογη με την απόλυτη θερμοκρασία δηλ. Π = kT όπου k = συντελεστής αναλογίας.

Ο van't Hoff διαπίστωσε ότι η ωσμωτική πίεση διαλύματος παρουσιάζει μεγάλη αναλογία με την πίεση που ασκεί ιδανικό αέριο και το οποίο υπακούει στην καταστατική εξίσωση : PV=nRT

Μετά από αυτές τις διαπιστώσεις ο van't Hoff διατύπωσε το "νόμο των αραιών διαλυμάτων" :
Η ωσμωτική πίεση αραιού διαλύματος είναι ίση με την πίεση που θα ασκούσαν τα μόρια της διαλυμένης ουσίας αν αυτά βρίσκονταν με τη μορφή ιδανικού αερίου, σε χώρο ίσου όγκου με το διάλυμα και σε ίση θερμοκρασία.

Για τα αραιά μοριακά διαλύματα θα ισχύει ο νόμος του van't Hoff^[5] (σε διάφορες μορφές) :

(ή αφού C = n/V)

(ή αφού n = m/M_r)

όπου :

Π = ωσμωτική πίεση (atm)

C = συγκέντρωση του διαλύματος (mol/L)

R = σταθερά των αερίων = 0.082 L.atm/mol.K

T = απόλυτη θερμοκρασία (Κ)

V = όγκος του διαλύματος (L)

n = αριθμός moles διαλυμένης ουσίας (mol)

m = μάζα διαλυμένης ουσίας (g)

M_r = σχετική μοριακή μάζα (g/mol)

Όπως φαίνεται από τις παραπάνω σχέσεις :

• Η ωσμωτική πίεση (Π) σε ορισμένη θερμοκρασία εξαρτάται από τον αριθμό γραμμομορίων ή μορίων του διαλυμένου σώματος σε ορισμένο όγκο διαλύματος και επομένως είναι μια προσθετική ιδιότητα δηλ. η τιμή της σε ορισμένη ποσότητα διαλύτη είναι ανεξάρτητη από τη φύση του διαλυμένου σώματος και εξαρτάται μόνο από το συνολικό αριθμό διαλυμένων σωματιδίων.


• Όταν ένα διάλυμα αραιώνεται, η συγκέντρωσή του ελαττώνεται και επομένως η ωσμωτική του πίεση επίσης ελαττώνεται. Το αντίθετο συμβαίνει σε διάλυμα που συμπυκνώνεται.


• Αν οι διαλυμένες ουσίες είναι πολλές, οι παραπάνω σχέσεις παίρνουν τις μορφές :

Π =(C₁+C₂+C₃+...)RT ⟺ ΠV = (n₁+n₂+n₃+...)RT = (m₁/M_r1 + m₂/M_r2 + m₃/M_r3 + ...)RT

2) Πυκνά μοριακά διαλύματα

Στα σχετικώς πυκνά διαλύματα παρατηρούνται σοβαρές αποκλίσεις από το νόμο του van't Hoff. Σ' αυτές τις περιπτώσεις πρέπει από το συνολικό όγκο του διαλύματος να αφαιρείται ο όγκος που καταλαμβάνουν αυτά τα ίδια τα μόρια της διαλυμένης ουσίας. Αντί λοιπόν του όγκου V του διαλύματος, λαμβάνεται ο όγκος του διαλύτη (V'). Η εξίσωση που προκύπτει είναι γνωστή ως εξίσωση Morse :

Νόμος του van't Hoff για την ωσμωτική πίεση σε διαλύματα ηλεκτρολυτών |

Στα ηλεκτρολυτικά διαλύματα η ωσμωτική πίεση (και γενικότερα οι προσθετικές ιδιότητες των διαλυμάτων) έχει μεγαλύτερη τιμή από εκείνη που προβλέπεται βάσει των εξισώσεων και της συγκέντρωσης του ηλεκτρολύτη. Έτσι, σε άλατα όπως NaCl, KNO₃ κ.ά. η πειραματική τιμή της Π βρέθηκε περίπου διπλάσια, σε άλατα του τύπου BaCl₂, Ca(NO₃)₂ κ,ά, περίπου τριπλάσια, σε άλατα του τύπου K₃[Fe(CN)₆] κ.ά. περίπου τετραπλάσια κλπ. Ο van't Hoff πρότεινε την εισαγωγή στις απλές εξισώσεις της ωσμωτικής πίεσης, ενός αδιάστατου διορθωτικού συντελεστή i που σήμερα ονομάζεται "συντελεστής van't Hoff" :

όπου :

i = συντελεστής van't Hoff

Π_ηλ = η ωσμωτική πίεση ηλεκτρολυτικού διαλύματος ορισμένης συγκέντρωσης

Π = η ωσμωτική πίεση μοριακού διαλύματος της ίδιας ακριβώς συγκέντρωσης.

Συνεπώς οι εξισώσεις γίνονται :

Βρέθηκε ότι ο i δεν είναι σταθερός για κάθε ηλεκτρολύτη, αλλά αυξάνεται με την αραίωση και τείνει σε ακέραιο αριθμό ίσο με τον αριθμό των ιόντων που υπάρχουν στο μόριο του ηλεκτρολύτη. Έτσι για το KCl που περιέχει δύο ιόντα : ΚCl → Κ⁺ + Cl^-, θα είναι i = 2 μόνο στην άπειρη αραίωση ενώ σε αραιό διάλυμα είναι περίπου 1,93. Αυτό οφείλεται στις λεγόμενες ιονικές έλξεις που παρεμποδίζουν την πλήρη διάσταση. Πάντως οι αποκλίσεις αυτές δεν είναι σημαντικές όταν τα διαλύματα είναι αραιά.

1) Διαλύματα ισχυρών ηλεκτρολυτών

Στα διαλύματα αυτά δεχόμαστε ότι η διάσταση του ηλεκτρολύτη είναι πλήρης και ο συντελεστής van't Hoff έχει ακέραια τιμή ίση με το άθροισμα των ιόντων που ο ηλεκτρολύτης αποδίδει σε πλήρη διάσταση. Έτσι για έναν ισχυρό ηλεκτρολύτη της μορφής ΚxAy (όπου Κ = κατιόν με αριθμό οξείδωσης +y και Α = ανιόν με αριθμό οξείδωσης -y) που διίσταται πλήρως κατά το σχήμα :

θα είναι i = x + y. Έτσι π.χ. για το Ca₃(PO₄)₂ → 3Ca⁺² + 2PO₄⁻³ θα είναι i = 3 + 2 = 5.

2) Διαλύματα ασθενών ηλεκτρολυτών

Στα διαλύματα αυτά ο ηλεκτρολύτης διίσταται μερικά και η τιμή της ωσμωτικής πίεσης είναι μεγαλύτερη από την αντίστοιχη μοριακού διαλύματος ίδιας συγκέντρωσης αλλά μικρότερη από την ωσμωτική πίεση ηλεκτρολυτικού διαλύματος ίδιας συγκέντρωσης.

Αν α είναι ο βαθμός διάστασης του ασθενούς ηλεκτρολύτη, τότε :

όπου n o αριθμός των ιόντων που δίνει ο ασθενής ηλεκτρολύτης κατά τον ιοντισμό του. Έτσι π.χ. για διάλυμα οξικού οξέος (CH₃COOH) στο οποίο το οξύ ιοντίζεται κατά 2 % (α = 0,02) σύμφωνα με το σχήμα : CH₃COOH ⇄ CH₃COO^- + H⁺ οπότε n = 2, ο i θα είναι : i = 1 - 0.02 + 2.0,02 = 1,02.

Η σχέση i = 1 - α + nα συνήθως χρησιμοποιείται γαι την εύρεση του α όταν πειραματικά υπολογίζεται ο i, οπότε έχει τη μορφή :

Η ωσμωτική πίεση στα πολυμερή |

Κατά τον πολυμερισμό ενός σώματος (συνήθως οργανικής ένωσης διαλυμένης σε οργανικό διαλύτη) γίνεται συνένωση μορίων του σώματος (μονομερή) και σχηματισμός μεγαλομορίων (πολυμερή). Άρα με τον πολυμερισμό ενός σώματος ελαττώνεται ο αριθμός των διακεκριμένων σωματιδίων του διαλύματος, οπότε ελαττώνεται και η ωσμωτική πίεση. Για παράδειγμα, έστω ότι πολυμερίζεται αιθυλένιο (μονομερές, CH₂=CH₂) αρχικής συγκέντρωσης C μέσα σε οργανικό διαλύτη. Αν ν μόρια αιθυλενίου συνενώνονται για να δώσουν πολυμερές (πολυαιθυλένιο) σύμφωνα με την αντίδραση :

η συγκέντρωση του μονομερούς θα είναι ν φορές μικρότερη δηλ. C/ν και επομένως η ωσμωτική πίεση θα είναι και αυτή ν φορές μικρότερη από την ωσμωτική πίεση του μονομερούς.

Ωσμώμετρο Pfeffer

Μέτρηση της ωσμωτικής πίεσης |

Η ωσμωτική πίεση υδατικών και μη διαλυμάτων μετριέται με συσκευές που λέγονται ωσμώμετρα. Το πρώτο ωσμώμετρο κατασκευάστηκε το 1828 από το Γάλλο φυσιολόγο Henri Dutrochet και δεν παρείχε ακριβείς μετρήσεις αλλά απλά μια επίδειξη της ώσμωσης. Ο Pfeffer κατασκεύασε το 1877 και χρησιμοποίησε για μετρήσεις ακριβείας, ωσμώμετρο που και σήμερα βρίσκει ακόμη εφαρμογή για μετρήσεις μικρών σχετικά ωσμωτικών πιέσεων : Το ωσμώμετρο Pfeffer αποτελείται από το πορώδες διάφραγμα Α και από υδραργυρικό μανόμετρο Β. Το κύτταρο που περιέχει το διάλυμα προς μελέτη τοποθετείται στο δοχείο Γ. Λόγω της ώσμωσης, ο διαλύτης εισέρχεται στο κύτταρο, οπότε η διαφορά στάθμης που δημιουργείται στο μανομετρικό σωλήνα δίνει την ωσμωτική πίεση του διαλύματος τη στιγμή αποκατάστασης ισορροπίας (σφού έχει εισέλθει ο διαλύτης) και όχι την ωσμωτική πίεση του αρχικού διαλύματος. Αν όμως παρεμποδίσουμε την είσοδο διαλύτη με προσθήκη υδραργύρου στο αριστερό σκέλος του μανόμετρου, τότε η διαφορά στάθμης που δημιουργείται θα δίνει την ωσμωτική πίεση του αρχικού διαλύματος. Η ωσμωτική πίεση σε KPa θα είναι Π = d.g.h όπου d = πυκνότητα υδραργύρου = 13,6 g/mL, g = βαρυτική επιτάχυνση = 9,81 m/s² και h = το ύψος της στήλης υδραργύρου (m). Με διαίρεση με το 100 προκύπτει η Π σε atm π.χ αν το ύψος h = 0.1 m τότε : Π = 13,6 × 9,81 × 0,1 = 13,3 KPa ή 0,133 atm.

Για μεγάλες ωσμωτικές πιέσεις (μέχρι 270 atm), οι Frazer και Myrick πρότειναν ειδικό ωσμώμετρο.

Εφαρμογές της ωσμωτικής πίεσης |

Ορισμένες από τις σημαντικότερες εφαρμογές της ωσμωτικής πίεσης είναι :

• Εύρεση της σχετικής μοριακής μάζας (M_r) μεγαλομοριακών ενώσεων (π.χ. πρωτεΐνες, πολυμερή) με τη μέθοδο της ωσμωμετρίας. Έτσι ονομάζεται η μέθοδος προσδιορισμού της M_r μιας ουσίας μετρώντας πειραματικά την ωσμωτική πίεση του υδατικού διαλύματός της. Η ωσμωμετρία εφαρμόζεται με την προϋπόθεση ότι το διάλυμα είναι αραιό και μοριακό. Για τον υπολογισμό χρησιμοποιείται η σχέση : M_r = mRT/ΠV. Η μέτρηση πρέπει όμως να γίνει σε κατάλληλες συνθήκες οι οποίες να μην ευνοούν τον πολυμερισμό (βλέπε #Η ωσμωτική πίεση στα πολυμερή).


• Υπολογισμός συγκέντρωσης διαλύματος ισότονου προς το αίμα. Η διαδικασία χρησιμοποιείται για την παρασκευή ορών διαφόρων ουσίων (π.χ. γλυκόζης, βιταμίνης C, φυσιολογικού ορού δηλ. διαλύματος NaCl 0,9 % κλπ.). Χρησιμοποιείται η σχέση : m = ΠVM_r/RT όπου Π = 6,74 atm που είναι η ωσμωτική πίεση του αίματος. Έτσι, αν θέλουμε να παρασκευάσουμε ισότονο ορό γλυκόζης (C₆H₁₂O₆, M_r = 180, μοριακή ουσία) θα πρέπει να διαλύσουμε m = 6,74.1.180/273.0,082 = 54,19 g γλυκόζης σε 1 L νερού στους 0 °C.

Ημιπερατές μεμβράνες |

Αναπαράσταση ημιπερατής μεμβράνης (με κίτρινο χρώμα) κατά τη διάρκεια της αιμοδιάλυσης. Κόκκινο = ερυθρά αιμοσφαίρια, μπλε = διαλυτικό υγρό

Οι ημιπερατές μεμβράνες, που ονομάζονται και ωσμωτικά διαφράγματα, επιτρέπουν τη δίοδο των μορίων του διαλύτη όχι όμως και των μορίων ή ιόντων της διαλυμένης ουσίας. Οι πόροι των μεμβρανών αυτών είναι γενικά μικρότεροι των 250 nm (250.10⁻⁹ m). Πολλές φυσικές, ιδίως ζωικές, μεμβράνες (κύστεις) μπορούν να χρησιμοποιηθούν σαν ημιπερατές μεμβράνες. Πολύ καλές μεμβράνες είναι επίσης πορώδεις πλάκες που περιέχουν στους πόρους τους δυσδιάλυτα άλατα.

Οι ημιπερατές μεμβράνες που χρησιμοποιούνται στην πράξη χωρίζονται σε δύο κατηγορίες :

• Διογκωμένα υλικά κολλοειδούς σύστασης όπως π.χ. η ζελατίνη, το ελαστικό κόμμι, η κυτταρίνη και τα παράγωγά της κ.ά.


• Μη διογκωμένα υλικά όπως π.χ. τα περισσότερα δυσδιάλυτα σύμπλοκα άλατα όπως είναι ο σιδηροκυανιούχος χαλκός, Cu₂[Fe(CN)₆], όταν βρίσκονται στους πόρους πορωδών δοχείων, το ωσμωτικό διάφραγμα Traube κ.ά.

Το σπουδαιότερο χαρακτηριστικό γνώρισμα κάθε ημιπερατής μεμβράνης είναι η διαπερατότητά της στα διάφορα μόρια ή σωματίδια. Η διαπερατότητα εξαρτάται από τη σύσταση της μεμβράνης και ιδίως από τις ηλεκτροχημικές ιδιότητές της. Η ιδιότητα που έχει μια ημιπερατή μεμβράνη να μην επιτρέπει τη δίοδο των μορίων της διαλυμένης ουσίας δεν οφείλεται στη διάμετρο των πόρων της μεμβράνης ή στο μέγεθος των μορίων της διαλυμένης ουσίας αλλά σε εκλεκτική παρεμπόδιση ηλεκτροχημικής κυρίως φύσης.

Βιολογική σημασία και εφαρμογές της ώσμωσης |

Το φαινόμενο της ώσμωσης παίζει σημαντικό ρόλο σε πολλά βιολογικά φαινόμενα που σχετίζονται με τη λειτουργία του κυττάρου. Τα κύτταρα περιέχουν σε μορφή υδατικού διαλύματος μόρια οργανικών ενώσεων (π.χ. πρωτεΐνες) και διάφορα άλατα η δε κυτταρική τους μεμβράνη είναι ημιπερατή.

Η ώσμωση στα φυτικά κύτταρα |

Φυτικά κύτταρα σε διαφορετικά περιβάλλοντα

Όταν ένα φυτικό κύτταρο βρεθεί σε νερό, το οποίο θεωρείται υποτονικό διάλυμα (hypotonic), ο όγκος του αυξάνεται και ταυτόχρονα πέφτει η ωσμωτική του πίεση, λόγω αραίωσης με την είσοδο του νερού. Με τη διόγκωση όμως του κυττάρου, το τοίχωμά του τεντώνεται πράγμα που συνεπάγεται μια ελαστική τάση της μεμβράνης που λέγεται σπαργή (turgid) αντίθετης κατεύθυνσης προς την ωσμωτική πίεση. Η ώσμωση αναστέλλεται, όταν η ελαστική τάση των τοιχωμάτων του κυττάρου εξισορροπήσει την ωσμωτική πίεση. Το φαινόμενο αυτό της διόγκωσης του φυτικού κυττάρου ονομάζεται σπάργωση.

Όταν το φυτικό κύτταρο βρεθεί σε υδατικό διάλυμα μεγαλύτερης ωσμωτικής πίεσης, δηλ. σε υπέρτονο διάλυμα (hypertonic), το νερό θα βγαίνει από το κύτταρο με αποτέλεσμα τη συρρίκνωση του κυττάρου. Το φαινόμενο αυτό λέγεται πλασμόλυση. Αν η πλασμόλυση δεν είναι πολύ ισχυρή ή δεν διαρκεί πολύ, είναι δυνατόν να επαναφέρουμε το κύτταρο στην αρχική φυσιολογική του κατάσταση με την τοποθέτησή του μέσα στο νερό. Το φαινόμενο αυτό λέγεται αποπλασμόλυση.

Η ώσμωση στα ζωικά κύτταρα |

Αποτελέσματα διαφορετικών διαλυμάτων στα ερυθρά αιμοσφαίρια

Στα ζωικά κύτταρα συμβαίνουν περίπου τα ίδια φαινόμενα που είναι όμως πιο έντονα. Και τα ζωικά κύτταρα μέσα σε υπέρτονα διαλύματα συρρικνώνονται, όμως στην περίπτωση αυτή αυξάνεται ο βαθμός διέγερσης και αντίδρασής τους και για αυτό ενέσεις υπέρτονων υδατικών διαλυμάτων είναι επικίνδυνες και προκαλούν ερεθισμούς. Αντίθετα, μέσα σε υποτονικά διαλύματα, τα ζωικά κύτταρα διογκώνονται και μειώνεται η διεγερσιμότητά τους. Αν η διόγκωση γίνει σε μεγάλο βαθμό, μπορεί να προκαλέσει τελικά την καταστροφή των ζωικών κυττάρων. Έτσι ενδοφλέβια ένεση υποτονικού διαλύματος είναι πολύ επικίνδυνη γιατί μπορεί να προκαλέσει διόγκωση και διάρρηξη των ερυθρών αιμοσφαιρίων. Το φαινόμενο αυτό λέγεται αιμόλυση.

Αν βάλουμε ερυθρά αιμοσφαίρια μέσα σε ισοτονικό υδατικό διάλυμα χλωριούχου νατρίου (NaCl) περιεκτικότητας 9 ‰, αυτά διατηρούν απόλυτα το σχήμα και το μέγεθός τους. Το ισότονο αυτό διάλυμα NaCl είναι γνωστό ως φυσιολογικός ορός.

Η ουρία είναι η μόνη ουσία που διέρχεται εντελώς ελεύθερα από τη μεμβράνη των ερυθρών αιμοσφαιρίων. Γι'αυτό το λόγο η ουρία μπορεί να προκαλέσει αιμόλυση ακόμα κι αν τα αιμοσφαίρια είναι μέσα σε ισότονο διάλυμα.

Ισότονο με το αίμα είναι και το υγρό των ιστών. Υπέρτονα με το αίμα είναι τα δάκρυα, ενώ υπότονα είναι το σάλιο και ο ιδρώτας. Τα ούρα μπορεί να είναι υπέρτονα ή και υπότονα.

Αιμοκάθαρση - Τεχνητός νεφρός |

Ο τεχνητός νεφρός είναι μια μηχανή που αποτελείται από ένα μεγάλο δοχείο, χωρητικότητας περίπου 100 L, μέσα στο οποίο τοποθετείται ένα διάλυμα ισοτονικό ως προς όλα τα συστατικά που πρέπει να παραμείνουν στο αίμα, το οποίο πρόκειται να καθαριστεί. Μέσα στο διάλυμα αυτό υπάρχει ένας μεγάλος σωλήνας με σπειροειδή μορφή που είναι φτιαγμένος από ένα είδος μεμβράνης η οποία επιτρέπει να περάσουν από τους πόρους της μόρια διαλύτη, ιόντα και άλλα μικρά μόρια που υπάρχουν στο αίμα. Το αίμα από μια αρτηρία του ασθενούς διοχετεύεται μέσα στο σωλήνα, οπότε τα τοξικά συστατικά που διέρχονται από τους πόρους της μεμβράνης προς το εξωτερικό διάλυμα απομακρύνονται και το καθαρισμένο πλέον αίμα εισάγεται ξανά στον ασθενή μέσα από μια φλέβα του.

Αντίστροφη ώσμωση |

Αναπαράσταση αφαλάτωσης θαλασσινού νερού με αντίστροφη ώσμωση

Όταν στο διάλυμα που έρχεται σε επαφή μέσω της ημιπερατής μεμβράνης με τον καθαρό διαλύτη ασκηθεί πίεση μικρότερη από την ωσμωτική πίεση του διαλύματος (δηλ. όταν P_εξ < Π), τότε στο διάλυμα θα συνεχίσει να εισέρχεται διαλύτης, αλλά με μικρότερο ρυθμό.

Όταν στο διάλυμα ασκηθεί εξωτερική πίεση μεγαλύτερη από την ωσμωτική πίεση του διαλύματος (δηλ. P_εξ > Π), τότε το φαινόμενο αντιστρέφεται και μόρια διαλύτη θα εξέρχονται από το διάλυμα προς τον καθαρό διαλύτη (ή από το πυκνότερο προς το αραιότερο διάλυμα). Το φαινόμενο αυτό λέγεται αντίστροφη ώσμωση. Με τον τρόπο αυτό αυξάνεται η συγκέντρωση του διαλύματος, αφού απομακρύνεται μέρος από την ποσότητα του διαλύτη.

Το φαινόμενο της αντίστροφης ώσμωσης βρίσκει εφαρμογή στην αφαλάτωση του θαλασσινού νερού για την αντιμετώπιση του προβλήματος της λειψυδρίας : Η ωσμωτική πίεση του νερού των ωκεανών είναι 27 atm. Αν ασκηθεί αρκετά μεγάλη εξωτερική πίεση (περίπου 70 atm), η ώσμωση μπορεί να σταματήσει και να αντιστραφεί, οπότε από τη μεμβράνη θα παρέχεται καθαρό νερό. Οι ημιπερατές μεμβράνες κατασκευάζονται από οξική κυτταρίνη ή από πολυαμίδια με τη μορφή μικροσκοπικών διάτρητων ινών. Το θαλασσινό νερό τροφοδοσίας εισάγεται υπό πίεση στις ίνες και εξέρχεται αφαλατωμένο. Η μεγαλύτερη εγκατάσταση αφαλάτωσης στον κόσμο βρίσκεται στη Σαουδική Αραβία όπου παράγεται το 50 % του νερού που καταναλίσκεται, με τη μέθοδο της αντίστροφης ώσμωσης. Τα τελευταία χρόνια η μέθοδος αυτή έχει εξαπλωθεί και σε πολλές πόλεις των Η.Π.Α. Για παράδειγμα στην πόλη Σάντα Μπάρμπαρα από το 1992 λειτουργεί εγκατάσταση αντίστροφης ώσμωσης για την παραγωγή 30400 m³ πόσιμου νερού τη μέρα.

Ανάλογες συσκευές, μικρής δυναμικότητας, είναι συχνά χειροκίνητες και χρησιμοποιούνται στα πλοία ή σε ορισμένες εγκαταστάσεις ξηράς π.χ. σε κάμπινγκ.

Σημειώσεις |

Πηγές |

• Γιαννακουδάκης Δ. Α. "Φυσική Χημεία Καταστάσεων της Ύλης και Θερμοδυναμική", Θεσσαλονίκη 1986.


• Γεωργάτσος Ι. Ε. "Βιοχημεία, Τόμος Α', Δομή μακρομορίων-Ένζυμα-Βιολογικές Οξειδώσεις", Θεσσαλονίκη 1985.


• Τρακατέλλης Α. "Βιοχημεία", Θεσσαλονίκη 1986.


• Γρανίτσας Α. Ν. "Βιολογία Τόμος Ι Βιολογία του Κυττάρου", Θεσσαλονίκη 1985.


• Μανωλκίδης Κ., Μπέζας Κ. "Στοιχεία Ανόργανης Χημείας", Έκδοση 14η, Αθήνα 1984.


• Γιαννακουδάκης Δ. Α. "Φυσική Χημεία Ομογενών και Ετερογενών Συστημάτων", Θεσσαλονίκη 1986.


• Μάτης Κ. Α., Γιαννακουδάκης Δ. Α. "Φυσικές Διεργασίες στη Χημική Τεχνολογία", Θεσσαλονίκη 1987.


• Μπαζάκης Ι. Α. "Γενική Χημεία", Αθήνα.


• Μανουσάκης Γ.Ε. "Γενική και Ανόργανη Χημεία", Τόμοι 1ος και 2ος, Θεσσαλονίκη 1981.

Εξωτερικοί σύνδεσμοι |

Το Βικιλεξικό έχει σχετικό λήμμα:   ώσμωση

Τα Wikimedia Commons έχουν πολυμέσα σχετικά με το θέμα    Ώσμωση

• Παραδείγματα ώσμωσης


• Πώς λειτουργεί η ώσμωση (video)


• Προσομοιώσεις ώσμωσης σε Java